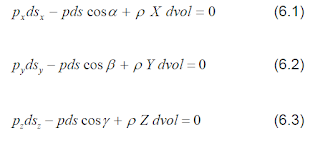Considérese un fluido en “reposo y en él una superficie diferencial ds (esto es tan pequeña como se quiera).
Dicha superficie ds divide al líquido en dos zonas (1) y (2), de tal modo que si se quisiese quitar la zona (1), para mantener el fluido en equilibrio, se tendría que hacer una fuerza dF , pues tanto las moléculas de la zona (1) como las de la (2) golpean a la otra a través de dicha superficie ds (ver Fig. 6.1).
Como se puede ver esta fuerza dF es perpendicular al elemento de área ds, y es que se ha dicho que el fluido está en “reposo” y por tanto no aparecerá una fuerza paralela al elemento de superficie ds, pues como se ha dicho la viscosidad o rozamiento entre capas fluidas es función de la velocidad relativa de éstas, y al acumularse dicha velocidad relativa se anula consecuentemente el rozamiento, con lo cual queda justificado el ángulo de 90º entre fuerza diferencial y superficie ds.
Se define la presión como:
o puesto vectorialmente:
La presión es una magnitud escalar, o dicho de otra forma no es un vector con módulo dirección y sentido, pues es independiente de la dirección que se considere como se va a demostrar a continuación.
Considérese un líquido en reposo y en su interior un tetraedro infinitesimal cuyas aristas, que parten del punto 0, son las infinitésimas. OA = dx; OB = dy y OC = dz, como muestra la Fig. 6.2.
Este tetraedro está en equilibrio bajo las fuerzas debidas a la presión en sus cuatro caras y las fuerzas por unidad de masa (en el caso del agua dentro de un depósito, la fuerza por unidad de masa, es la aceleración de la gravedad
por la masa diferencial.
Habrá, así, cinco fuerzas:
1. La primera que actuará sobre la cara OBC, de área ds, y en la cual actuará un presión p, y consecuentemente la fuerza será pds y formará su recta de acción ángulos α, β y γ con los ejes x, y y z respectivamente, como se puede ver en la Fig. 6.2.
2. La segunda fuerza debida a la presión actuará sobre la cara abc de área dsx y de valor
3. La tercera fuerza actuará sobre la cara OAC de área dsy y de valor
4. La cuarta fuerza actuará sobre la cara OAB y de valor
5. La quinta fuerza será la debida a la masa diferencial dm = ρ.dvol, donde ρ es la densidad y dvol el volumen del tetraedro diferencial OABC.
De esta forma si la fuerza por unidad de masa tiene por componentes X, Y y Z, la fuerza total sobre el elemento OABC será ρXdvol, ρYdvol, ρZdvol. X, Y y Z se unidan en N/kg o bien su equivalente m/seg2.
Proyectando las cinco fuerzas sobre los tres ejes coordenadas e imponiendo las condiciones de equilibrio al tetraedro se tendrá:
Analícese la ecuación (6.1):
Teniendo en cuenta que α es el ángulo que forma la fuerza pds con el eje x, y puesto que esta fuerza es normal al plano (pues no hay viscosidad) se cumple que α también es el ángulo que forma el área ds con el plano y o z y por tanto ds cosα = dsx . De esta forma la ecuación (6.1) queda:
Con lo cual simplificando: