Se llama fuerza centrípeta a la fuerza, o al componente de la fuerza que actúa sobre un objeto en movimiento sobre una trayectoria curvilínea, y que está dirigida hacia el centro de curvatura de la trayectoria.
El término (centrípeta) proviene de las palabras latinas centrum, (centro) y petere, (dirigirse hacia), y puede ser obtenida a partir de las leyes de Newton. La fuerza centrípeta siempre actúa en forma perpendicular a la dirección del movimiento del cuerpo sobre el cual se aplica. En el caso de un objeto que se mueve en trayectoria circular con velocidad cambiante, la fuerza neta sobre el cuerpo puede ser descompuesta en un componente perpendicular que cambia la dirección del movimiento y uno tangencial, paralelo a la velocidad, que modifica el módulo de la velocidad.
La fuerza centrípeta no debe ser confundida con la fuerza centrífuga, tal como se explica en la sección Malentendidos comunes.
Fuerza Centralita en la Mecánica
Los objetos con movimiento rectilíneo uniforme tienen una velocidad constante; pero un objeto que se mueva sobre una trayectoria circular con velocidad constante experimenta continuamente un cambio en la dirección de su movimiento, esto es, en la dirección de la velocidad. Puesto que la velocidad cambia, existe una aceleración. La magnitud de este cambio de dirección de la velocidad por unidad de tiempo es la aceleración centrípeta, representada por un vector dirigido hacia el centro de la circunferencia dado por
Donde:
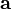==> es la aceleración centrípeta.
==> es el módulo de la velocidad.
==> es el radio de la trayectoria circular (en general, el radio de curvatura).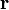
==> el vector de posición.
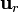==> el versor radial.
==> la velocidad angular.
Según la segunda ley de Newton, para que se produzca una aceleración debe actuar una fuerza en la dirección de esa aceleración. Así, si consideramos una partícula de masa en movimiento circular uniforme, estará sometida a una fuerza centrípeta dada por:
Ejemplo 1
Una pequeña esfera de 200 g de masa gira en una trayectoria circular de 0,8 m de radio con una velocidad angular de 5 rad/s. Calcular la magnitud de la fuerza centrípeta que actúa sobre la esfera.
SOLUCIÓN
Datos:
m = 200 g = 0,2 kg
R = 0,8 m
w = 5 rad/s
La ecuación a utilizar es:
Fcp = m acp = m w2 R
Reemplazando los datos:
Fcp = (0,2)(5)2 (0,8)
Fcp = 4 N
Ejemplo 2
Una masa de 100 g atada a una cuerda de 50 cm de longitud gira en un plano vertical. Si cuando pasa por el punto más bajo su velocidad es de 3 m/s, ¿qué valor tiene la tensión de la cuerda en ese instante? Considere: g = 10 m/s2.
SOLUCIÓN
Datos:
m = 100 g = 0,1 kg; R = 50 cm = 0,5 m; v = 3 m/s
Dibujemos el diagrama de cuerpo libre de la masa:
La fuerza centrípeta es la resultante de las dos fuerzas radiales (fuerzas que se encuentran en la dirección del radio), entonces:
Fcp = T - mg
Aplicando la segunda ley de Newton:
Fcp = m a cp
Luego:
T - mg = m v2/R
Reemplazando datos:
T - (0,1)((10) = (0,1)(32)/0.5
T - 1 = 1,8
T = 2,8 N