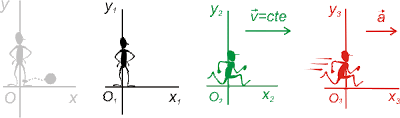El movimiento siempre es un concepto relativo porque debe referirse a un sistema de referencia o referencial particular escogido por el observador. Puesto que diferentes observadores pueden utilizar referenciales distintos, es importante relacionar las observaciones realizadas por aquellos.
Ejemplo.
Una partícula se encuentra en movimiento en un referencial si su posición con respecto a él cambia en el transcurso del tiempo; en caso contrario, la partícula está en reposo en dicho referencial. De estas definiciones, vemos que tanto el concepto de movimiento como el de reposo son relativos. Así, el pasajero que está sentado en un vagón de ferrocarril se encuentra en reposo con respecto al vagón; pero como el tren se mueve con respecto a la Tierra, el pasajero se encuentra en movimiento con respecto a los árboles que observa desde el tren. A su vez, esos árboles están en reposo respecto de la Tierra, pero en movimiento respecto del pasajero del tren.
Existen dos tipos de sistemas de referencia:
- Sistema de referencia inercial: es aquél que está en reposo o se mueve con velocidad constante (es decir, no tiene aceleración).
- Sistema de referencia no inercial: es aquél que tiene aceleración.
Los vectores posición, velocidad y aceleración de una partícula tendrán en general distinto valor dependiendo del sistema de referencia desde el que estén calculados.
Es interesante disponer de ecuaciones que relacionen los valores de dichos vectores calculados desde distintos sistemas de referencia, porque de este modo, una vez calculados con respecto a uno de ellos y conociendo el movimiento relativo de ambos sistemas de referencia, podremos obtener los vectores medidos por el segundo.
En esta sección vamos a obtener dichas ecuaciones para varias situaciones concretas: cuando los dos sistemas de referencia se encuentran en movimiento relativo de traslación (uniforme y uniformemente acelerado) y cuando se encuentran en movimiento relativo de rotación uniforme.
Movimiento relativo de traslación uniforme
Las transformaciones de Galileo son las ecuaciones que relacionan los vectores de posición, velocidad y aceleración medidos desde dos sistemas de referencia diferentes, cuando uno de ellos está en reposo y el otro se mueve con velocidad constante con respecto al primero. Es importante resaltar que en esta situación ambos sistemas de referencia son inerciales.
Movimiento relativo de traslación uniforme. O y O' son dos sistemas de referencia inerciales, y O' se mueve con velocidad V constante con respecto a O.
En la figura anterior está representada la trayectoria de una partícula (en azul) y los dos sistemas de referencia junto con los vectores unitarios que definen los sentidos positivos de sus ejes. Como puede observarse,
vector posición
derivando se tiene vector velocidad
derivando de nuevo tenemos vector aceleración
Movimiento relativo de traslación uniformemente acelerado
Consideremos ahora una situación semejante a la anterior, pero en la que el sistema que se traslada lo hace con una aceleración constante A con respecto al que permanece en reposo.
Según las relaciones del movimiento uniformemente acelerado la distancia recorrida por O´ en un tiempo t es ahora:
De forma análoga al caso anterior obtenemos las siguientes relaciones:
vector posición
derivando tenemos vector velocidad
derivando de nuevo tenemos vector aceleración
Es decir, las aceleraciones mediadas por ambos sistemas no coinciden.
- Un sistema que se encuentra en movimiento relativo acelerado con respecto a otro es un sistema de referencia no inercial.
- Un sistema de referencia no inercial se denomina así porque en él no se cumple la ley de inercia o Primera Ley de Newton.