La energía potencial gravitacional es la energía que posee un objeto, debido a su posición en un campo gravitacional. El uso mas común de la energía potencial gravitacional, se da en los objetos cercanos a la superficie de la Tierra donde la aceleración gravitacional, se puede presumir que es constante y vale alrededor de 9.8 m/s2. Puesto que el cero de energía potencial gravitacional, puede elegirse en cualquier punto (como la elección del cero de un sistema de coordenadas), la energía potencial a una altura h por encima de ese punto es igual al trabajo que sería requerido para elevar el objeto a esa altura sin cambio neto en su energía cinética. Puesto que la fuerza requerida para elevar un objeto es igual a su peso, se sigue que la energía potencial gravitacional es igual a su peso multiplicado por la altura a la que se eleva.
Por ejemplo, si un libro apoyado en una mesa es elevado, una fuerza externa estará actuando en contra de la fuerza gravitacional. Si el libro cae, el mismo trabajo que el empleado para levantarlo, será efectuado por la fuerza gravitacional.
Por esto, un libro a un metro del piso tiene menos energía potencial que otro a dos metros, o un libro de mayor masa a la misma altura.
Si bien la fuerza gravitacional varía junto a la altura, en la superficie de la Tierra la diferencia es muy pequeña como para ser considerada, por lo que se considera a la aceleración de la gravedad como una constante ( 9,8 m/s2) en cualquier parte. En cambio en la luna, cuya gravedad es muy inferior, se generaliza el valor de 1,66 m/s2
Para estos casos en los que la variación de la gravedad es insignificante, se aplica la fórmula:
Donde 
es la energía potencial, 
la masa,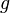 
la aceleración de la gravedad, y 
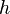la altura.
es la energía potencial, la masa, 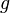la aceleración de la gravedad, y 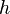la altura.
Sin embargo, si la variación de altitud es importante, y por tanto la variación de la aceleración de la gravedad es considerable, se aplica la fórmula general:
Donde 
es la energía potencial, 
es la distancia entre la partícula material y el centro de la Tierra,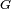 
la constante universal de la gravitación y 
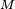la masa de la Tierra. Esta última es la fórmula que necesitamos emplear, por ejemplo, para estudiar el movimiento de satélites y misiles balísticos:
es la energía potencial, es la distancia entre la partícula material y el centro de la Tierra, 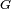la constante universal de la gravitación y 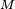la masa de la Tierra. Esta última es la fórmula que necesitamos emplear, por ejemplo, para estudiar el movimiento de satélites y misiles balísticos:
Una forma de energía potencial es la que está asociada con el campo gravitacional, que hace efecto en los cuerpos por medio de su peso.Ésta es la energía potencial gravitatoria Ug, que relaciona el peso de un cuerpo y su altura sobre el suelo.
Para encontrar su valor, considere un cuerpo de masa m que está en reposo a una altura h(1), como se muestra en la figura. La única fuerza que actúa sobre el cuerpo es su peso w = m*g. Entonces, el trabajo neto sobre ella es:
Wg = m*g*d.
Donde d es la distancia en la que se aplica la fuerza.
Si el objeto se deja caer hasta la altura h(2), entonces d = h(1) - h(2):
Wg = m*g*(h(1) - h(2))
La energía potencial gravitatoria Ug se define como el producto de la masa por la aceleración de la gravedad por la altura h:
Ug = m*g*h
Entonces el trabajo es:
Wg = m*g*h(1) - m*g*h(2) = Ug(1) - Ug(2)
Si ∆Ug = Ug(2) - Ug(1):
Wg = - ∆Ug
Ésta relación sólo es válida para el trabajo realizado por la fuerza de la gravedad.
Campo gravitatorio
La interacción atractiva que experimentan entre sí los cuerpos materiales dotados de masa responde, desde un punto de vista teórico, a la existencia de un campo gravitatorio asociado a toda masa no nula. Las fuerzas asociadas a este campo fueron descritas por la ley de gravitación universal de Newton (ver t21), y de su estudio se dedujo que eran directamente proporcionales a las masas afectadas por el fenómeno gravitatorio e inversamente proporcionales a la distancia que separa a dichas masas.
Líneas de campo gravitatorio
Los campos vectoriales se representan mediante series de líneas que señalan la trayectoria que seguirían las partículas bajo la influencia del campo. En el campo gravitatorio creado por una masa puntual, estas líneas de fuerza siguen direcciones que apuntan hacia la masa creadora del campo.
Aunque la Tierra tiene forma de geoide ligeramente achatado por los polos, se puede considerar que es un planeta esférico y que la distribución de su masa es uniforme. Entonces, se considera también que engendra un campo gravitatorio regular cuyas líneas de fuerza apuntan hacia el centro de la Tierra. Por convenio, se dice que este campo es negativo, por lo que la expresión de su intensidad sería la siguiente:
siendo M+ = 5,98 · 1024 kg. En la superficie terrestre, la distancia considerada es igual al radio de la Tierra R+ =6.370 km, con lo que la fuerza que ejerce la Tierra sobre una masa m situada en esta posición se calcula según la conocida expresión:
El vector g se conoce como intensidad del campo gravitatorio terrestre local o, simplemente, gravedad.
A todo campo vectorial se le asocia una energía potencial o capacidad que tiene dicho campo para realizar trabajo según la posición de las partículas dentro del mismo. En el campo gravitatorio terrestre local, la energía potencial gravitatoria asociada tiene la forma:
con z la altura de la partícula (masa puntual) considerada sometida a la acción del campo según el eje de referencia escogido.
Por la equivalencia entre trabajo y energía, la energía potencial gravitatoria del campo terrestre local puede determinarse como el producto escalar de la fuerza ejercida por la distancia recorrida, con lo que se obtiene que:
